One Sample Z test for proportion is applied to test whether a sample proportion in significantly different than a known / hypothesized proportion, when N * P1/100 > 5.

Steps:

1. Null hypothesis and Alternate Hypothesis

Null Hypothesis

A. Two tailed test: Sample proportion is equal to hypothesized proportion. OR Sample proportion is not significantly different than hypothetical proportion.

B. One tailed test: (Right tailed): Sample proportion is not more than hypothesized proportion. OR Sample proportion is equal to or less than hypothesized proportion.

C. One tailed test: (Left tailed): Sample proportion is not less than hypothesized proportion. OR Sample proportion is equal to or more than hypothesized proportion.

 Alternate Hypothesis

A. Two tailed test: Sample proportion is significantly different than hypothetical proportion.

B. One tailed test: (Right tailed): Sample proportion is significantly more than hypothesized proportion.

C. One tailed test: (Left tailed): Sample proportion is significantly less than hypothesized proportion.

2. Calculate Test statistics Z

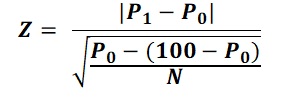
where Z is the test statistics,
P₁ = Sample proportion, (In percentage)
P₀ = hypothesized / known / population proportion, (In percentage)
N = Sample Size

If proportions are out of 1, then replace 100 with 1 in above equation.

3. Know p value from Z table

4. Interpret

If p < = alpha, then reject Null hypothesis, and accept alternate hypothesis.

If p > alpha, then the study has failed to reject Null hypothesis. So accept Null hypothesis.

---

---

Example 1:

A random sample of 50 newborn babies in a city has shown that 13 of them were LBW babies. Apply an approriate statistical test to test whether the proportion of LBW babies in the city is significantly different than population proportion of 20%, at alpha level of 5%.

Here, we want to compare a sample proportion with population. We can apply "One Sample Z test for proportion." We could have also applied "Chi square test of Goodness of fit."
Here,
P₀ = 20%, P₁= 13*100 /50 = 26%, N =50, alpha = 5%, tails = 2 (significantly different)
Putting above values at the respective places, we get the output as follows:

p = 0.2888. P value is not statistically significant at given alpha level of 0.05 (5%). Sample proportion is not significantly different than hypothesized / known proportion.

Sample Proportion = 26
Hypothesized / known Proportion = 20
Z = 1.06066017177982
p = 0.288844422304211 (Two tailed)
Alpha = 0.05 (5 %). Critical Z value = 1.95996398451889
95 % Confidence interval = 13.8419024754233 to 38.1580975245767.

---

Example 2:

A random sample of 50 newborn babies in a city has shown that 13 of them were LBW babies. Apply an approriate statistical test to test whether the proportion of LBW babies in the city is significantly more than population proportion of 20%, at alpha level of 5%.

Here, we want to compare a sample proportion with population. We can apply "One Sample Z test for proportion." We could have also applied "Chi square test of Goodness of fit."
Here,
P₀ = 20%, P₁= 13*100 /50 = 26%, N =50, alpha = 5%, tails = 1 (significantly more)
Putting above values at the respective places, we get the output as follows:

p = 0.1444. P value is statistically insignificant at given alpha level of 0.05 (5%). Sample proportion is not significantly more than hypothesized / known proportion.

Sample Proportion = 26
Hypothesized / known Proportion = 20
Z = 1.06066017177982
p = 0.144422211152105 (One tailed)
Alpha = 0.05 (5 %). Critical Z value = 1.64485362699727
95 % Confidence interval = 15.7966029127849 to ∞.

---

---