Example:
A researcher wants to conduct a study to predict the marks obtained in final examination by students. His predictor (independent) variables are physical attendance in percentage, score in pre-final examination, gender and score in a separate IQ test. What is the size of the sample required to achieve 80% power for a multiple regression on these 4 independent variables at confidence level of 95%? A pilot study has revealed R2 = 0.24.
Solution:
Here
Confidence level = 95%, power = 80%, R2=0.24, k=4
After putting these values, we get required sample size = 43.
How sample size is calculated? (Exclusively for advanced users)
1. Calculation of sample size for Simple / Multiple Linear Regression requires a complex iterative approach.
2. Initially iteration process is started at temporary predecided lowest sample size = k + 2.
3. Starting with the lowest sample size (N) of k + 2 , degrees of freedom for numerator (k) and denominator (N-k-1) are calculated. Then using given confidence level and these degrees of freedom, F critical value is calculated. For example, if the number of predictors are 4, then we will start with sample size of 6. In this case, degrees of freedom for numerator (d1) will be k = 4. Degrees of freedom for denominator (d2) will be N – k -1 =1. Now F critical value (x) for 95% confidence level (alpha=0.05), 4 and 1 degrees of freedom is calculated using inverse F distribution function. (It is the F table value for given alpha and degrees of freedom). In this case,critical F value will be 224.5832
4. Non centrality parameter λ (lambda) is calculated using following equation.
λ = f2 * N
. If effect size input is R2 or η2 or f, then f 2 is calculated as follows
f2 = R2/ (1 - R2)
f2 = η2/ (1 - η2)
f2 = f * f
5. Using the values of non-centrality parameter (λ), d1, d2 and x; power of the test is calculated using non central cumulative distribution function formula.
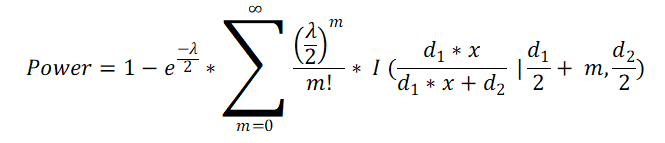
Where, I (q | a, c) is the regularized incomplete beta function.
6. If calculated power is less than desired, process is repeated by increasing the sample size by 1, till the desired power is achieved.
@ Sachin Mumbare