Example:
A researcher wants to test whether level of education is significantly associated with hypertension. During literature search, he found one similar study, the findings of the same were as follows:
|
Illiterate |
Primary |
Secondary |
Graduates |
Postgraduates |
Total |
| Hypertensives |
10 |
15 |
12 |
25 |
38 |
100 |
| Normotensives |
30 |
32 |
28 |
45 |
15 |
150 |
| Total |
40 |
47 |
40 |
55 |
68 |
250 |
How much sample size is required to test the association at 95% confidence level, power of 80% and he wants to include equal number of hypertensives and normotensives in the study?
Solution
Initially, we need to calculate row percentages of above data to use them as input. Following table shows the row percentages.
|
Illiterate |
Primary |
Secondary |
Graduates |
Postgraduates |
Total |
| Hypertensives |
10 (10.00%) |
15(15.00%) |
12(12.00%) |
25(25.00%) |
38(38.00%) |
100(100.00%) |
| Normotensives |
30(20.00%) |
32(21.333%) |
28(18.667%) |
45(30.00%) |
15(10.00%) |
150(100.00%) |
| Total |
40 |
47 |
40 |
70 |
53 |
250 |
Then, we need to input the given information in the appropriate places, as follows.
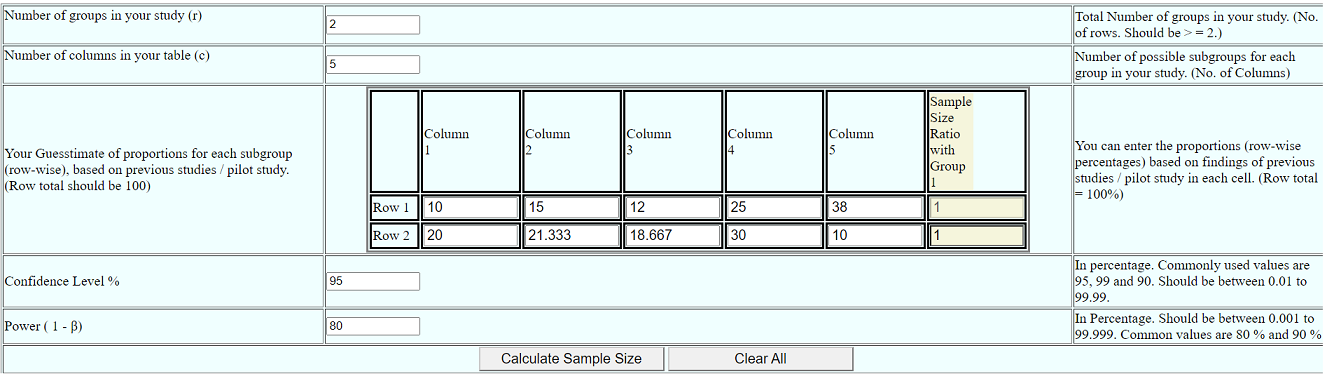
After clicking "Calculate Sample Size" we get the sample size equal to 52 in each group. (Total sample size = 52 * 2 = 104)
How sample size is calculated? (Exclusively for advanced users)
1. Calculation of sample size required for Chi-Square test of independance requires a complex iterative approach.
2. Initially sample size = r * c * 5 is temporarily decided, to maintain expected value of minimum 5 in most of the cells.
3. Degrees of freedom(df) is calculated as (r -1) * (c - 1).
4. Based on degree of freedom and confidence level, critical chi-square value (x) is calculated. For example, if df = 3. Critical chi-square value, for confidence level of 95% (or alpha of 5%) and df =3, is 7.815. (It is the chi-square table value for given alpha and degrees of freedom)
5. Based on initial sample size of r * c * 5 and given proportions for each cell, observed and expected values are calculated for each cell.
6 A. Chi-square value for each cell is calculated using following formula. This chi-square value is also equal to the non-centrality parameter
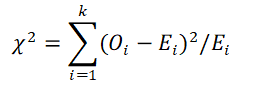
6 B. Alternatively non centrality parameter (lambda) can also be calculated using following formula.
λ = N * w ^2
Where w is the effect size, N is the sample size. w is calculatd as follows.

Where P1i is the proportion under alternate hypothesis in group i (Guesstimate of observed proportions). P0i is the proportion under null hypothesis in group i (expected proportions)
7. Using the values of non-centrality parameter (λ), df and x; power of the test is calculated using non central chi square cumulative distribution function formula.
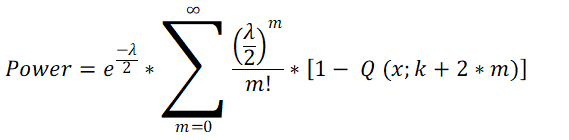
Where, Q (x, k + 2 * m) is the CDF of central chi-square distribution with critical value of x and df of k + 2 * m .
6. If calculated power is less than desired, process is repeated by increasing the sample size, till the desired power is achieved.
@ Sachin Mumbare