Example:
A researcher wants to find whether there is significant difference in proportions of various blood groups amongst doctors. A pilot study has revealed that the proportions of blood groups A, B, AB and O amongst doctors are 25, 35, 10 and 30 respectively. The expected proportions as per population data are 20, 25, 5 and 50 respectively. How much sample size is required, if confidence level is 95%, intended power is 80 %.
Solution:
Here
Confidence level = 95%, power = 80%, H0_1=20%, H0_2=25%, H0_3=5%, H0_4=50%, H1_1=25%, H1_2=35%, H1_3=10%, H1_4=30%
After putting these values, we get required sample size in each group = 60.
How sample size is calculated? (Exclusively for advanced users)
1. Calculation of sample size required for Chi-Square GoF requires a complex iterative approach.
2. Initially sample size = r * 5 is temporarily decided, to maintain expected value of minimum 5 in most of the cells.
3. Based on the number of groups / levels in group (k) degrees of freedom(df) is calculated as k -1.
4. Based on degree of freedom and confidence level, critical chi-square value (x) is calculated. For example, if the number of groups / levels are 4, then df = 3. Critical chi-square value for confidence level of 95% (or alpha of 5%) and df =3 is 7.815. (It is the chi-square table value for given alpha and degrees of freedom)
5. Based on initial sample size of r * 5 and given proportions for each cell, observed and expected values are calculated for each cell.
6 A. Chi-square value for each cell is calculated using following formula. This chi-square value is also equal to the non-centrality parameter
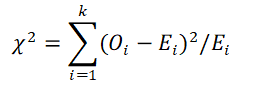
6 B. Alternatively non centrality parameter (lambda) can also be calculated using following formula.
λ = N * w ^2
Where w is the effect size, N is the sample size. w is calculatd as follows.

Where P1i is the proportion under alternate hypothesis in group i (Guesstimate of observed proportions).Where P0i is the proportion under null hypothesis in group i (expected proportions)
7. Using the values of non-centrality parameter (λ), df and x; power of the test is calculated using non central chi square cumulative distribution function formula.
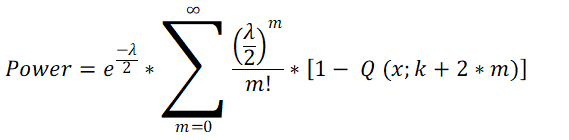
Where, Q (x, k + 2 * m) is the CDF of central chi-square distribution with critical value of x and df of k + 2 * m .
6. If calculated power is less than desired, process is repeated by increasing the sample size in first group by 1, till the desired power is achieved.
@ Sachin Mumbare