Example:
A researcher wants to find whether there is significant difference in mean heights of adults from four different ethnic backgrounds. Previous studies have revealed the mean heights to be 165 ± 10 cm, 168 ± 10 cm, 175 ± 11 cm, and 169 ± 11 cm. How much sample is required, if confidence level is 95% and intended power is 80 % and equal sample size in all four groups.
Solution:
Here
Confidence level = 95%, power = 80%, M1 = 165, SD1= 10, M2=168, SD2=10, M3=175, SD3=11, M4=169, SD4=11.
After putting these values, we get required sample size in each group = 24. (Total sample size = 24 * 4 = 96)
How sample size is calculated? (Exclusively for advanced users)
1. Calculation of sample size for ANOVA requires a complex iterative approach.
2. Starting with the lowest sample size =2 in first group, sample size in each group is temporarily decided as per the SS ratio with first group.
3. Based on this sample size, degrees of freedom for numerator and denominator are calculated. Then using given confidence level and these degrees of freedom, F critical value is calculated. For example, if the number of groups are 3, and SS ratio for each group is 1, then we will start with sample size of 2 in each group. In this case, degrees of freedom for numerator (d1) will be k -1 = 3 -1 =2. Degrees of freedom for denominator (d2) will be N – k = 3*2 – 3 = 3 (k = number of groups, N = total sample size in all k groups). Now F critical value (x) for 95% confidence level, 2 and 3 degrees of freedom is calculated using inverse F distribution function. (It is the F table value for given alpha and degrees of freedom)
4. Non centrality parameter (lambda) is calculated using following equation.
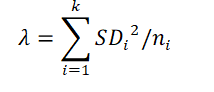
5. Using the values of non-centrality parameter (λ), d1, d2 and x; power of the test is calculated using non central cumulative distribution function formula.
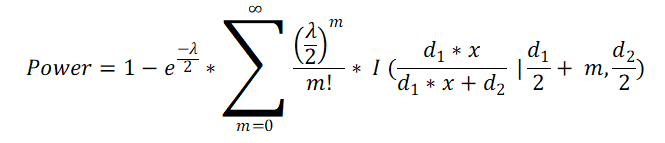
Where, I (q | a, c) is the regularized incomplete beta function.
6. If calculated power is less than desired, process is repeated by increasing the sample size in first group by 1, till the desired power is achieved.
@ Sachin Mumbare