Example:
A researcher conducted a study to predict the marks obtained in final examination by students. His predictor (independent) variables were physical attendance in percentage, score in pre-final examination, gender and score in a separate IQ test. He conducted the study with inclusion of 25 randomly selected students, and an effect size, R2 = 0.24. What was the power of the study to detect that these 4 independent variables were significant predictors of the dependent variable, at confidence level of 95%?
Solution:
Here
Confidence level = 95%, N = 25, R2=0.24, k=4
After putting these values, we get Power = 48.98%.
How power for simple or multiple regression is calculated? (Exclusively for advanced users)
1. Calculation of sample size for Simple / Multiple Linear Regression requires a complex approach.
2. Based on given sample size (N) and number of predictors (k) , degrees of freedom for numerator (k) and denominator (N-k-1) are calculated. Then using given confidence level and these degrees of freedom, F critical value is calculated. For example, if the number of predictors (k) = 4, and sample size = 6; degrees of freedom for numerator (d1) will be k = 4. Degrees of freedom for denominator (d2) will be N – k -1 =1. Now F critical value (x) for 95% confidence level (alpha=0.05), 4 and 1 degrees of freedom is calculated using inverse F distribution function. (It is the F table value for given alpha and degrees of freedom). In this case,critical F value will be 224.5832
3. Non centrality parameter λ (lambda) is calculated using following equation.
λ = f2 * N
. If effect size input is R2 or η2 or f, then f 2 is calculated as follows
f2 = R2/ (1 - R2)
f2 = η2/ (1 - η2)
f2 = f * f
4 Using the values of non-centrality parameter (λ), d1, d2 and x; power of the test is calculated using non central cumulative distribution function formula.
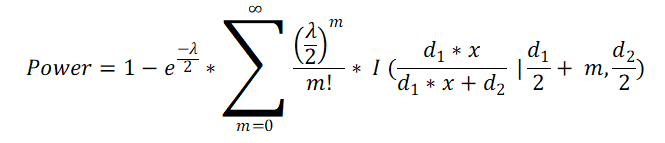
Where, I (q | a, c) is the regularized incomplete beta function.
@ Sachin Mumbare