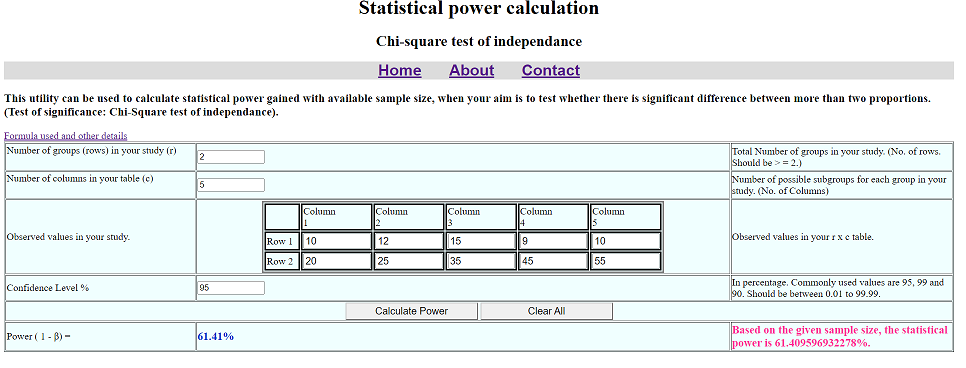
Example:
A researcher wants to find whether there is significant association between level of maternal education and birth weight of new borns. The study revealed following findings. How much was the power of the study to find association between maternal education and birth weight?
| |
Illiterate |
Primary |
Secondary |
Graduate |
Post Graduate |
Total |
| Low birth weight babies |
10 |
12 |
15 |
9 |
10 |
56 |
| Normal birth weight babies |
20 |
25 |
35 |
45 |
55 |
180 |
| Total |
30 |
27 |
50 |
54 |
65 |
226 |
Solution:
Here, r = 2, c= 5. (Please do not count row or column for totals)
After putting these values, we get power = 61.41%.
Illustrative screenshot:
How sample size is calculated? (Exclusively for advanced users)
1. Calculation of sample size required for Chi-Square test of independence requires a complex approach.
2. Based on the number of groups (rows: r) and number of colums (c) degrees of freedom(df) is calculated as (r-1)*(c-1)
3. Based on degree of freedom and confidence level, critical chi-square value (x) is calculated. For example, if r = 4, and c = 2, then df = 3 * 1 = 3. Critical chi-square value for confidence level of 95% (or alpha of 5%) and df =3 is 7.815. (It is the chi-square table value for given alpha and degrees of freedom)
4. Based on given observed values, expected values for each cell are calculated using the formula
Ei = RTi * CTi / N. Where RTi and CTi are the row total and column total for observation i. N is the grand total.
5. A. Chi-squares value is calculated using the formuls
Where Oi and Ei are observed and expected values for each cell.
B. Alternately Chi-square value can also be calculated directly, without need of expected value, using Mumbare's method.
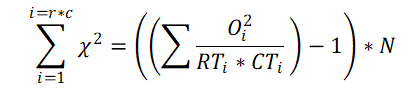
The chi-square value is also equal to the non-centrality parameter
7. Using the values of non-centrality parameter (λ), df and x; power of the test is calculated using non central chi square cumulative distribution function formula.
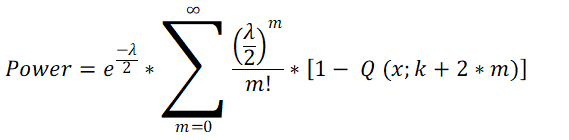
Where, Q (x, k + 2 * m) is the CDF of central chi-square distribution with critical value of x and df of k + 2 * m .
@ Sachin Mumbare