Meta-analysis of prospective studies (effect size = Risk Ratio, Relative Risk)

The meta-analysis can be done using following models.

1. Fixed effect model
2. Random effects model

Selection of appropriate model depends upon the heterogeneity amongst the included studies. (see below for details)

Fixed effect meta-analysis: Steps

Treated Group Control Group Total
Events a c a + c
No Events b d b + d
total a + b c + d N

1. Calculating / extracting effect size: RR for each included studies. (RR = Relative Risk or Risk Ratio)

RR = Incidence in treated group / Incidence in control group  = (a/(a+b))/ (c/(c+d))
Incidence in treated group = Number of events in treated group /Total number of persons (or person-times) in treated group = a/(a+b)
Incidence in control group = Number of events in control group /Total number of persons (or person-times) in control group = c/(c+d)
(For observational prospective or cohort studies: treated group ~ cohort group.)

2. Calculating LogeRR for each included studies. (Log Relative Ratio base e)

3. Calculating Variance (V) and Standard Error of Log (RR)

Variance (V) = (1/a - 1/(a+b) + 1/c - 1/(c+d))
SELog RR = sqrt((1/a - 1/(a+b) + 1/c - 1/(c+d))

4. Calculating confidence intervals for Log (RR) and converting them to original scale.

A. Confidence intervals for Log RR
LB CI = Log (RR) - Z1-α/2 * SE Log RR
UB CI = Log (RR) + Z1-α/2 * SE Log RR

B. Confidence intervals of RR
We can convert above confidence intervals into original scale by following formula.
RR = eLog RR

5. Weights (W) of each included studies under fixed effect model (inverse variance method)

W = 1/V

6. Summary Log RR (meta-analysis Log RR) under fixed effect model is calculated as follows


MALog RR = Summary Log RR
Wi= Weight for ith included study
Yi= Log RR for ith included study

7. Standard Error of MALog RR = 1/Σ Wi

Once summary Log RR and its standard error is calculated, it is fairly easy to calculate confidence intervals of Log RR.
We can convert summary Log RR and its confidence intervals into original scale as described above under point 4(B).

8. Z value and p value.

Once summary Log RR and its standard error is calculated, it is fairly easy to calculate Z value and p value using normal distribution.
Z = MALog RR / Standard Error of MALog RR

If available data is Relative Risk and its confidence interval, then log RR is initially calculated. SE of log RR is calculated from UB and LB of confidence intervals, as follows.

SELog RR = (UBLog RR - Log RR) / Z1−α/2
It can be also calculated as follows
SELog RR = (Log RR - LBLog RR) / Z1−α/2
Variance (V) = SE2


Measures of heterogeneity

Not all included studies are homogeneous with respect to characteristics of participants such as age, gender, geo-environmental factors, other socio-demographic factors, selection criteria for cases etc. When these differences are present, variability in the study results is not just random, and the studies are considered as heterogeneous. This heterogeneity is quantified by following measures of heterogeneity.

1. Cochran's Q statistics

Q = Σ Wi * (Yi - M)2
Yi = Log RR for ith study
M = Summary Log RR (Meta-analysis Log RR)

Q statistics follows chi-square distribution with k - 1 degrees of freedom (k= number of included studies)
So, p value for Cochran's Q statistics can easily be calculated using chi square distribution.
Significant p value indicates that significant heterogeneity is present, and we should consider other methods of meta-analysis like random effects model or sub-group analysis or meta-regression.

2. Tau squared (τ2) statistics

τ2= (Q - (k -1)) / C
where,
C = Σ Wi - Σ Wi 2 / Σ Wi
Σ Wi = Sum total of weights of all included studies
Σ Wi2 = Sum total of squared weights of all included studies

3. I2 statistics

I2= 100 * (Q - (k -1)) / Q
I2 statistics is measured in percentage. I2 value of < 25% is considered as low heterogeneity, between 25 and 50 it is moderate and above 50% it is significant heterogeneity.

All above measures of heterogeneity provides a quantified measure, but they can not identify the factors causing heterogeneity.

Random effects model

If fixed effect meta-analysis shows significant heterogeneity (by Cochran's Q or I2 as explained above), then random effects model is one way to deal with heterogeneity.
In random effects model (DerSimonian‐Laird), weights of each study are revised as follows .
WRE = 1/ (V + τ2)

There are other methods used for random effects model such as maximum likelihood, restricted maximum likelihood (REML), Paule‐Mandel, Knapp‐Hartung etc. However, DerSimonian‐Laird method is most widely used and robust.

Then, summary Log RR (meta-analysis Log RR) under random effects model is calculated as follows


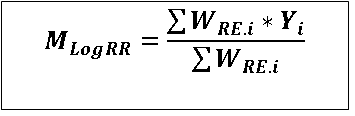
MALog RR = Summary Log RR
WRE.i= Revised weight for ith included study
Yi= Log RR for ith included study

 Standard Error of MALog RR = 1/Σ WRE.i

Once summary Log RR and its standard error is calculated, it is fairly easy to calculate confidence intervals of Log RR.
We can convert summary Log RR and its confidence intervals into original scale as described above under point 4(B).

Z value and p value.

Once summary Log RR and its standard error is calculated, it is fairly easy to calculate Z value and p value using normal distribution.
Z = MALog RR / Standard Error of MALog RR

Prediction interval is calculated using following formula.


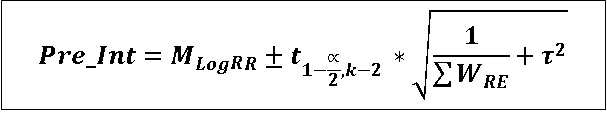
Where, t1-α/2, k-2  is (1−α/2)% percentile of t distribution with significance level α and k−2 degrees of freedom, (k = number of studies included in the meta-analysis).

Interpretation: There is a 95% (or any other specified) probability that a newly conducted study will have effect size between this interval.


Galbraith Plot

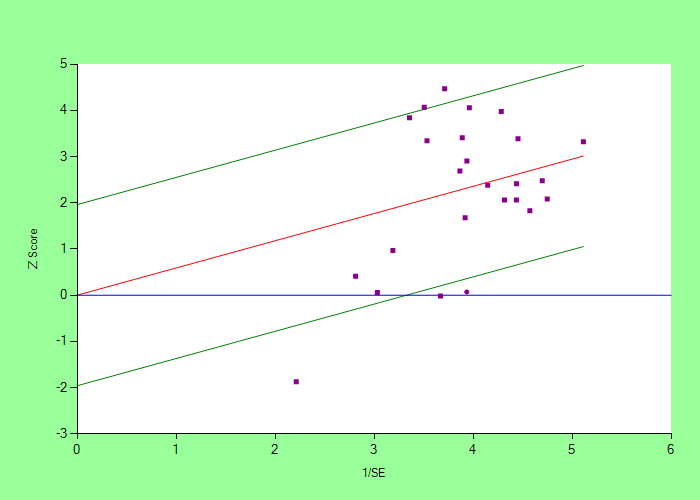
The Galbraith plot can also provide graphical representation to assess heterogeneity in the included studies.
It is a scatter plot of Z value against precision (1/SE) of each included studies. (Z value of each study = Log RR / SELog RR).
The central horizontal blue line represents the line of null effect (Log RR = 0). Studies above this line has Log RR > 0 or (RR > 1). Studies below this line has Log RR < 0.
Middle red line represents the MA Log RR. Its slope is equal to the MA Log RR. Studies above this line has Log RR > MA Log RR. Studies below this line has Log RR < MA Log RR.
Two green line (above and below middle red line), represents the confidence intervals of MA Log RR.
In the absence of significant heterogeneity, we expect that about 95% (or other specified level) studies lie between the two green lines, and 5% (or other specified level) lie outside this. If more number of studies are outside these lines, then it indicates significant heterogeneity.
In this Galbraith plot, two studies are above the top green line and three studies are below bottom green line. So a total of 5 studies, out of 25 included studies are not within the zone bounded by two green lines, suggesting heterogeneity.

Forest Plot

The forest plot represents RR of each included study with its confidence interval. It provides collective and comprehensive graphical view of all included studies as well as Meta-analysis summary RR.
Each horizontal line represents the confidence interval of the corresponding study. Diamond at the centre on each line represents the RR reported by the study. The thickness of the diamond is proportional to the RR.
Vertical line corresponding to RR = 1, represents line of null effect. It also signifies that the studies towards left of it has shown RR < 1, whereas studies towards right has shown RR > 1. If horizontal line for any included study does not cross this vertical line, it means the corresponding study has reported significant RR.

Forest plot also provides degree of overlap between included studies (to judge heterogeneity) and precision (as judged by the length of confidence interval) of each included study.
Bottom horizontal line with central rectangle represents MA RR and its confidence interval.
For random effects model, additional horizontal line is shown, which represents the prediction interval. It can be used to predict the results of newly conducted study. This interval tells us that about 95% (or other specified level) newly conducted studies will show effect size within this interval.

Sensitivity Analysis

The sensitivity analysis is done for each included studies by repeating meta-analysis after excluding one study at a time.
This forest plot of sensitivity analysis (one study removed) shows the MA RR and its confidence interval, when the corresponding study is removed and MA is performed with remaining studies. In this example, the horizontal line corresponding to study MA25 (top horizontal line) shows results of Meta-analysis after study MA25 is removed and meta-analysis is performed using remaining 24 studies.
Similarly line corresponding to MA1 represents shows results of Meta-analysis after study MA1 is removed and meta-analysis is performed using remaining 24 studies.
This sensitivity analysis shows the "influence" of each included study on the original meta-analysis. If after removal of a study, the results are showing substantial change, it tells that the study has significant impact on the results of original meta-analysis,
For example, in this example, no study shows significant impact, as after removal of any study,  the MA RR has not changed substantially.

Publication bias

It is a common tendency of publishers to publish "significant" studies. In other words, if result of a research is statistically non-significant, then such study can miss publication (file drawer problem). Meta-analysis includes mainly published studies, so it is often biased towards positive results. This bias is called as publication bias. The publication bias can be assessed by asymmetry of funnel plot, Begg-Mazumdar rank correlation test, Egger's regression test, Fail-Safe N, Duval and Tweedie trim and fill method.

Funnel Plot

Funnel plot is scatter plot of Effect Size (Log RR) and its Standard Error. To keep the bigger studies (with small SE) at the top, the Y axis is inverted, as shown here. So, the studies at the top are big (small SE) and studies at the bottom are small (large SE). As the studies at the bottom have large SE, to be significant they require to have larger effect size. So, the studies tend to scatter widely from top to bottom, resembling to shape of a funnel. In the absence of any publication bias, the studies are expected to spread symmetrically around central vertical line, which corresponds to the MA Log RR. In presence of significant publication bias, there will be asymmetrical spread of studies, particularly at the bottom. So, a careful assessment of the symmetry of funnel plot can tell us about the presence of publication bias.

In this example, if we look at the bottom, we can assess that 1 "extra" study is seen there to the left side. Corresponding or "mirror" study on the right is not seen. This has caused asymmetry of the plot, suggesting presence of possible publication bias.

Note: Two other lines, on either side of central vertical lines are just guiding line to ease the assessment of asymmetry. Different softwares use different slopes for these lines, so these lines should never be used at "cut-off line" to assess asymmetry.

Begg and Mazumdar rank correlation test

Begg and Mazumdar rank correlation
Kendall's S Statistics -10
Kendall's tau without continuity correction
(* significant p value indicates significant publication bias)
Kendall's Tau -0.033
Z -0.234
p (one tailed) 0.408
Kendall's tau with continuity correction
(* significant p value indicates significant publication bias)
Kendall's Tau -0.03
Z -0.21
p (one tailed) 0.417

Funnel plot can suggest possible publication bias, but it tends to have subjective variations. Begg and Mazumdar rank correlation test can tell us objectively about the presence of publication bias. This test uses non-parametric rank correlation test based on Kendall's tau.
The power of the test is less, so significance level is often taken as twice of the intended significance level (0.1 instead of 0.05).
In this example, p value is 0.408 (without continuity correction) and 0.417 (with continuity correction). Here, p value is more than the revised significance level of 0.1 for the test, we can conclude that there is no significant publication bias.

Egger's regression test

Egger's regression test
(* significant p value indicates significant publication bias)
Intercept -2.293
Standard error of intercept 1.727
t value -1.328
df 23
p (one tailed) 0.0986
LB of Confidence interval -5.865
UB of confidence interval 1.2786

Another significance test to detect publication bias is Egger's regression test. This test calculates the intercept of simple linear regression of Z score against precision (1/SE). The significant p value suggests presence of publication bias. Though the power of Egger's regression test is more than Begg and Mazumdar's rank correlation test, cut-off p value is often doubled.
Here, p value is 0.0986, more than the cut-off value of 0.05.This suggests absence of significant publication bias.

Fail-Safe N (Rosenthal)

Fail-Safe N (Rosenthal)
Z value for observed studies 11.674
P value for observed studies (two tailed) 0
Alpha 0.05
Z for given alpha (one tailed) 1.6449
Z for given alpha (two tailed) 1.96
Fail-Safe N (One tailed) 1137
Fail-Safe N (Two tailed) 793

Orwin's Fail-Safe N
Effect Size in meta-analysis Risk Ratio = 1.8025
Criteria for trivial effect Size
Average effect size for missing studies
Orwin's Fail-Safe N
266

Another method to assess publication bias is to calculate Fail-Safe N. We know that, publication bias is a result of non-publication of certain studies, mainly due to non-significant studies. It tends to bias the results positively or away from null effect. If we could find all such "missing" studies and add to the meta-analysis, then our meta-analysis or summary effect size will be reduced, may be to the extent that it is no more significant. But finding such "missing" or "unpublished" studies is practically not possible. Alternately, we can calculate number of additional studies with average null effect required to be added to the meta-analysis to change the summary effect size to non-significant level. If such number of "missing" or "unpublished" studies, with average null effect size, required to change the p value to non-significant level, is small, then publication bias is considered. Here, we can infer that with addition of small number of possible missing or unpublished studies , the summary effect size will become non-significant. On the other hand, if such number of "missing" or "unpublished" studies are large, then safely we can conclude that there is no serious problem of publication bias. (To decide whether Fail-Safe N is small or large, it should be judiciously compared with number of studies available in the literature / included in the meta-analysis)
Classical Fail-Safe N (described by Rosenthal)
It is equal to the number of such "missing" or "unpublished" studies, with average null effect size, required to be added to the meta-analysis, to change the summary effect size to non-significant level.
In this example, the p value provided by meta-analysis is < 0.001. We will need additional 793 studies, with average null effect size, to bring the p value above 0.05 (two tailed).
Orwin's Fail-Safe N
It is an alternative to classical Fail-Safe N. Classical Fail-Safe N gives number of studies required to bring down the results to non-significant level. Orwin's Fail-Safe N gives number of additional studies, required to bring down the summary effect size to a specified level (trivial criteria). Additionally, we can specify the average effect size of missing studies(M).
In this example, the summary RR was 1.8025. If trivial RR value is considered as 1.1, and average RR in "missing" or "unpublished" studies is taken as 1.05, then we will require 266 more such studies to be added to meta-analysis to bring down the summary RR to 1.1. (You can change these criteria and re-calculate the Orwin's Fail-Safe N. Needless to say that, the trivial effect size criteria must be less than the MA summary effect size and average effect size must be less than trivial criteria.)

Duval and Tweedie Trim and Fill

Duval and Tweedie's Trim and Fill
Number of studies trimmed and filled Risk Ratio LB RR UB RR
Meta-analysis Results   1.803 1.633 1.99
Left sided missing studies adjusted 0 1.8025 1.6328 1.99
Right sided missing studies adjusted 1 1.836 1.664 2.025



While, all above methods of detection of publication bias can suggest or detect it, none of them gives the actual impact of probable publication bias. Trim and fill method actually detects the publication bias by detecting asymmetry of funnel plot, identifies studies that are causing asymmetry, trims (removes) those studies and finally adds these trimmed studies along with hypothetical studies which are "mirror" images of trimmed studies. Mirror image study means a hypothetical study towards the opposite side, at equivalent distance from the central MA summary measure. This will make the funnel plot symmetrical. This "fill" of mirror images is based on the consideration that these are the probable studies which are missed publication. That is why this method is called as "Trim and Fill" method. Finally, after filling of probable missed studies, meta-analysis is done again.

This revised estimate of meta-analysis, after adding hypothetical and probable missed studies, will give us the summary measure equal to what we would have got, had there was no publication bias. If the difference between original meta-analysis and after "Trim and Fill" is large, we can conclude that the impact of publication bias is significant. If the difference is minimal, we can conclude that the impact is minimal.
We will learn this method using the same funnel plot given above. The method has detected that there is no "missing" study on left side, which is causing funnel plot asymmetry. (Actually tere is one "extra" study on left side. See below). So, no study is added to the left side. Hence, revised estimates are same as the original estimates. Funnel plot is also the same, without adding any "mirror" image study.

 The method has identified one "missing" study on right side, (as there is one "extra" study on left side), which is causing funnel plot asymmetry. So, the method has added 1 hypothetical study (red dot) on right side, which is mirror image of  "identified extra study on left side". After adding this hypothetical study, meta-analysis is revised, and revised estimates of summary measures are provided in the table. Original estimates of RR were 1.803 (1.633 - 1.99), and revised estimates are 1.836 (1.664 - 2.025). This change in overall estimates is very minimal.

Final remarks on publication bias:

In above example, Funnel plot has suggested the possibility of publication bias. Whereas Begg Mazumdar test and Egger's regression test have not suggested any significant bias. Fail-Safe N value is 793 and 266. Trim and Fill has identified publication bias and has given its possible impact. Now, the question is how to interpret these contradictory findings? Here, we should compare Fail-Safe N with number of available studies in meta-analysis(793 or 266 versus 25). When, 25 studies are detected by our search, is it possible to have another > 250 "missing" studies? The answer is, not likely! The required number > 250 is huge as compared with available 25 studies. Secondly, "Trim and Fill" has shown 1 extra study, but even after adding hypothetical study to make funnel plot symmetrical, there is no substantial change, quantitatively or qualitatively, in the final results of the meta-analysis. So, safely we can conclude that there is no impact of publication bias.

L'abb´e Plot

The L’Abb´e plot is a scatterplot of the log risk in the controls and treated group on the x axis and the y axis, respectively. (Risk = Incidence rate = number of events / total number of persons or person-times ) The log risks are plotted as circles with their sizes proportional to study size or precision (1/SE).
The central thin pink reference line is the line of similar outcomes in control and treated group. If a study has equal log risk in controls and treated, the circle corresponding to this study will lie on this line. If a study has larger log risk for treated than controls, then the circle will lie above the line. If a study has larger log risk for controls than treated, then the circle will lie below the line.
The other line represents estimated overall effect-size line. This plot can be used to explore heterogeneity by outlying studies. How?
It is expected that, all the studies will follow the overall effect-size line. Studies far away from this line suggest heterogeneity. Additionally, as the sizes of circles represent the study size (or precision), we can have an idea about "pull" phenomenon caused by such large study.
In this L'abb´e plot, the studies are spread around the overall effect size line, suggesting possible heterogeneity.

If available data is in the form of RR and its confidence interval, then we do not have incidence rates (risks) in treated and controls. So, L'abb'e plot can not be generated.

@ Sachin Mumbare